Cart-pole Swing-up Task Using MPC
By Bolun Dai | Apr 20th 2022
In this blog, I want to swing-up a cart-pole system using a model predictive control (MPC) based method. When I was initially shown this problem, I thought this was a toy problem and I will be able to solve in a few minutes. Then I realized that in school, all I have been taught was about linear MPC, and for cartpole related problems all I know is how to balance it on the top, assuming that it starting close to the top, so that the linearization is still valid. As for the case of swinging-up the cartpole, this stems firmly in the realm of nonlinear control. Which I have also learned. One of the more classical ways to deal with this would then be to linearize along the trajectory, such as using iLQR. However, when given state and control constraints, e.g. limit control effort and not letting the cartpole sway to far, iLQR losses its appeal. There are ways to incorporate constraints into iLQR, such as
I then did some reading and I found a way to do constrained nonlinear control: using direct collocation
Introduction
Now let’s first define the system and the problem. The dynamics of the cart-pole system can be defined as
\[\dot{\mathbf{x}} = \begin{bmatrix} \dot{x}\\ \dot{\theta}\\ \ddot{x}\\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{x}\\ \dot{\theta}\\ \frac{m_p\sin{\theta}(l\dot{\theta}^2 + g\cos{\theta})}{m_c + m_p\sin^2{\theta}}\\ \frac{-m_pl\dot{\theta}^2\cos{\theta}\sin{\theta} - (m_c + m_p)g\sin{\theta}}{l(m_c + m_p\sin^2{\theta})} \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \frac{1}{m_c + m_p\sin^2{\theta}}\\ \frac{-1}{l(m_c + m_p\sin^2{\theta})} \end{bmatrix}u,\]where \(m_c\) is the weight of the cart, \(m_p\) is the weight of the pole, \(\ell\) is the length of the pole, \(x\) is the center of mass position of the cart, \(\theta\) is the orientation of the pole and \(u\) is the control action which in this case is a force acting on the cart. The control problem is to swing-up the pole till it balances at the upright position. This can be captured using the following cost function
\[J = \int_{0}^{T}{(\mathbf{x}(t) - x^*)^TQ(\mathbf{x}(t) - x^*) + u(t)^TRu(t)dt},\]where \(Q\) and \(R\) are weight matrices, \(T\) is the preview horizon and \(x^*\) is the target state, which in this case is \([1,\ \pi,\ 0,\ 0]^T\). To make the problem more realistic, the cart position and control efforts are all constrained, i.e. \(x\in[-a,\ a]\) and \(u\in[-b,\ b]\). This problem is a nonlinear constrained optimization problem which is quite hard to solve, if written as-is I don’t even know how to give it to a solver (if anyone reading this has a solution please let me know). In the next section, we will look into how using a trapezoidal collocation method we can transform the problem into something more tractable.
Trapezoidal Collocation
The key idea here is to approximate integrals using trapezoidal quadrature. There are other ways to approximate it, as mentioned in

Here we can use the system dynamics \(\dot{x} = f(x)\) as an example. If we want to integrate the system dynamics from \(t_k\) to \(t_{k+1}\),
\[\int_{t_k}^{t_{k+1}}{\dot{x}} = \int_{t_k}^{t_{k+1}}{f(x)},\]is equivalent to calculating the area under the curve \(f(x)\) from \(t_k\) to \(t_{k+1}\). Which we can easily see can be approximated by a trapezoidal quadrature denoted by the yellow region. Using the formula of trapezoidal area we can get an approximation of the system dynamics
\[\int_{t_k}^{t_{k+1}}{\dot{x}} = \frac{t_{k+1} - t_k}{2}\Big(f(x(t_k)) + f(x(t_{k+1}))\Big) \approx x(t_{k+1}) - x(t_k),\]where the last approximation is obtained by the fundamental theorem of calculus. By discretizing the system dynamics and cost function using a trapezoidal approximation we can easily write out the aforementioned nonlinear constrained optimization problem, which we will discuss in the next section.
Reformulation
Using the aforementioned trapezoidal approximation, we can transform the cost from an integration over the entire trajectory to a summation at a few states, which are called knot points. The step-wise cost is
\[w(t) = (\mathbf{x}(t) - x^*)^TQ(\mathbf{x}(t) - x^*) + u(t)^TRu(t).\]If we take the integral between \(t_k\) and \(t_{k+1}\) we have
\[\int_{t_k}^{t_{k+1}}{w(t)dt} \approx \frac{t_{k+1} - t_k}{2}\Big(w(t_k) + w(t_{k+1})\Big).\]If we pick a series of timesteps \(h_k = t_{k+1} - t_k\), for the entire preview horizon we can have
\[\int_{0}^{T}{w(t)dt} = \sum_{i=0}^{N-1}{\frac{h_k}{2}\Big(w(t_k) + w(t_{k+1})\Big)}.\]Similarly, to ensure the state dynamics are respected, an equality constraint needs to be added. Following the same formulation as the last section we have a set of equality constraints, one at each knot point,
\[\frac{h_k}{2}\Big(f(x(t_k)) + f(x(t_{k+1}))\Big) = x(t_{k+1}) - x(t_k), \forall i = 1, \cdots, N-1.\]Now we can write out the reformulated problem
\[\begin{align*} \min_{x(\cdot), u(\cdot)}\ &\ \sum_{i=0}^{N-1}{\frac{h_k}{2}\Big(w(t_k) + w(t_{k+1})\Big)}\\ s.t.\ &\ \frac{h_k}{2}\Big(f(x(t_k)) + f(x(t_{k+1}))\Big) = x(t_{k+1}) - x(t_k)\\ &\ -\mathbf{a} \leq x(t_k) \leq \mathbf{a}\\ &\ -b \leq u(t_k) \leq b.\\ &\ x_0 = 0, \forall i = 1, \cdots, N-1. \end{align*}\]For the original direct collocation approach, the cost is only the control squared and there is an additional terminal state constraint. However, in a MPC framework, this approach is too “fragmented”. Intuitively, one can think that under such a setup, in order the minimize the cost, it would be best to plan to only reach the top at the end of the preview horizon. Since in MPC the preview horizon is moving, this will make the system never attempt to actually reach the target, but always “preparing” to.
Results
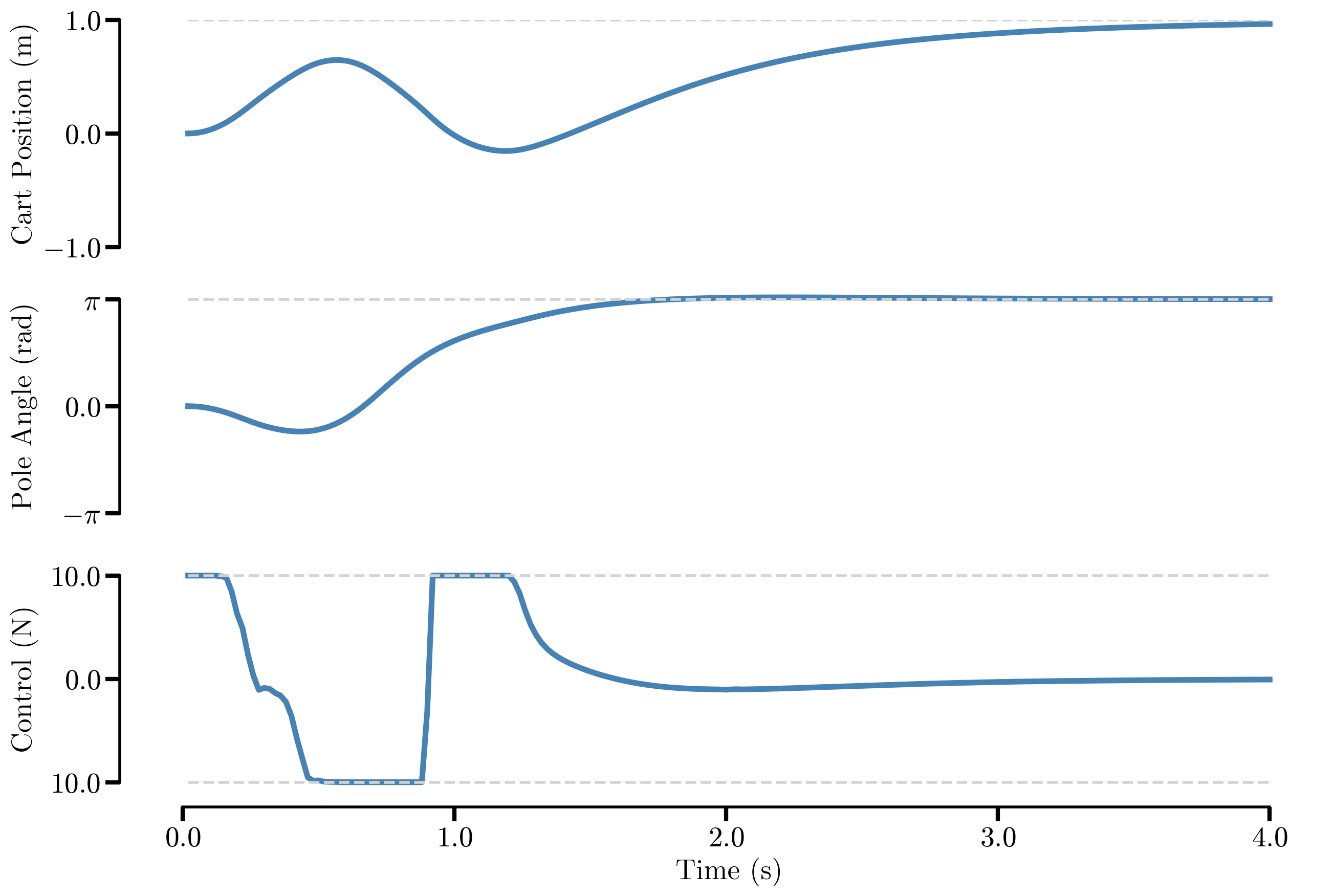
Using the aforementioned approach we can see that the cart-pole system is able to balance at the top. The control is saturated at 10N. The target is \([1.0,\ \pi,\ 0.0,\ 0.0]\). Though not shown here, the simulation is ran for 10 seconds and the pole is firmly balanced at the top. We see that this approach truly is able to solve the cartpole swing-up task. One thing to note is that when running SQP there is no need to run till a solution is found, in this case only four iteration is allowed at each timestep.
A few notes on the implementation. I implemented this in Matlab, due to not being able to get scipy’s optimization package to work, while fmincon works right out the box, credit to Mathworks. If anyone is able to get this working on scipy please let me know, I am dying to know what I did wrong. To ensure the system dynamics are as close to reality as possible, it was integrated using ode45. This shows that even if the dynamics are simplified when using trapezoidal collocation, the resulting control is still adequate in dealing with real dynamics.
